cse230
Excerpt
UCSD CSE 230
Recap: Haskell Crash Course II
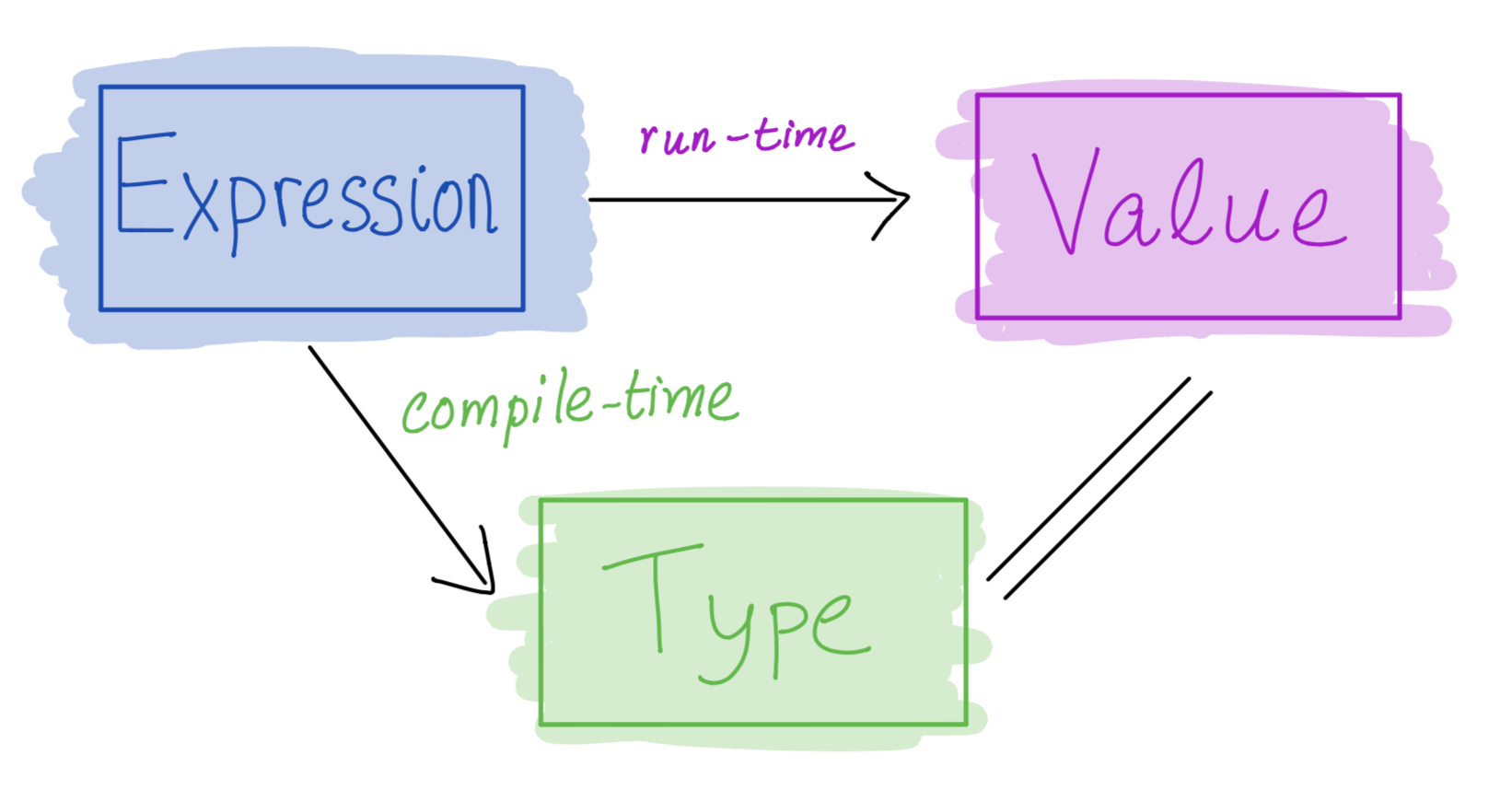
- Core program element is an expression
- Every valid expression has a type (determined at compile-time)
- Every valid expression reduces to a value (computed at run-time)
Recap: Haskell
Basic values & operators
Int,Bool,Char,Double+,-,==,/=
Execution / Function Calls
- Just substitute equals by equals
Producing Collections
- Pack data into tuples & lists
Consuming Collections
- Unpack data via pattern-matching
Next: Creating and Using New Data Types
-
typeSynonyms: Naming existing types -
datatypes: Creating new types
Type Synonyms
Synonyms are just names (“aliases”) for existing types
- think
typedefinC
A type to represent Circle
A tuple (x, y, r) is a circle with center at (x, y) and radius r
type Circle = (Double, Double, Double)
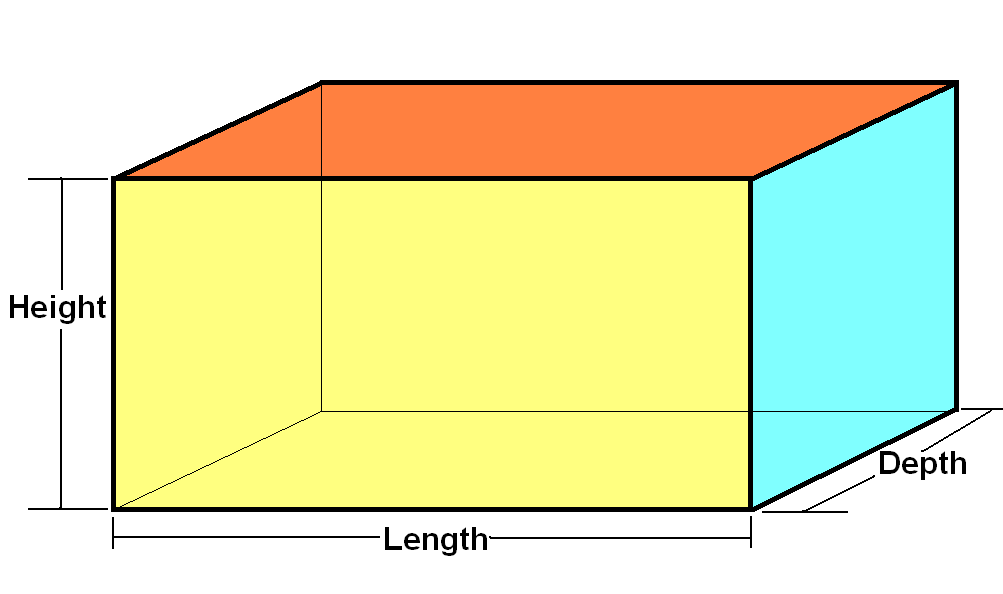
A type to represent Cuboid
A tuple (length, depth, height) is a cuboid
type Cuboid = (Double, Double, Double)
Using Type Synonyms
We can now use synonyms by creating values of the given types
circ0 :: Circle
circ0 = (0, 0, 100) -- ^ circle at "origin" with radius 100
cub0 :: Cuboid
cub0 = (10, 20, 30) -- ^ cuboid with length=10, depth=20, height=30
And we can write functions over synonyms too
area :: Circle -> Double
area (x, y, r) = pi * r * r
volume :: Cuboid -> Double
volume (l, d, h) = l * d * h
We should get this behavior
>>> area circ0
31415.926535897932
>>> volume cub0
6000
QUIZ
Suppose we have the definitions
type Circle = (Double, Double, Double)
type Cuboid = (Double, Double, Double)
circ0 :: Circle
circ0 = (0, 0, 100) -- ^ circle at "origin" with radius 100
cub0 :: Cuboid
cub0 = (10, 20, 30) -- ^ cuboid with length=10, depth=20, height=30
area :: Circle -> Double
area (x, y, r) = pi * r * r
volume :: Cuboid -> Double
volume (l, d, h) = l * d * h
What is the result of
A. 0
B. Type error
Beware!
Type Synonyms
-
Do not create new types
-
Just name existing types
And hence, synonyms
- Do not prevent confusing different values
Creating New Data Types
We can avoid mixing up by creating new data types
-- | A new type `CircleT` with constructor `MkCircle`
data CircleT = MkCircle Double Double Double
-- | A new type `CuboidT` with constructor `MkCuboid`
data CuboidT = MkCuboid Double Double Double
Constructors are the only way to create values
-
MkCirclecreatesCircleT -
MkCuboidcreatesCuboidT
QUIZ
Suppose we create a new type with a data definition
-- | A new type `CircleT` with constructor `MkCircle`
data CircleT = MkCircle Double Double Double
What is the type of the MkCircle constructor?
A. MkCircle :: CircleT
B. MkCircle :: Double -> CircleT
C. MkCircle :: Double -> Double -> CircleT
D. MkCircle :: Double -> Double -> Double -> CircleT
E. MkCircle :: (Double, Double, Double) -> CircleT
Constructing Data
Constructors let us build values of the new type
circ1 :: CircleT
circ1 = MkCircle 0 0 100 -- ^ circle at "origin" w/ radius 100
cub1 :: Cuboid
cub1 = MkCuboid 10 20 30 -- ^ cuboid w/ len=10, dep=20, ht=30
QUIZ
Suppose we have the definitions
data CuboidT = MkCuboid Double Double Double
type Cuboid = (Double, Double, Double)
volume :: Cuboid -> Double
volume (l, d, h) = l * d * h
What is the result of
>>> volume (MkCuboid 10 20 30)
A. 6000
B. Type error
Deconstructing Data
Constructors let us build values of new type … but how to use those values?
How can we implement a function
volume :: Cuboid -> Double
volume c = ???
such that
>>> volume (MkCuboid 10 20 30)
6000
Deconstructing Data by Pattern Matching
Haskell lets us deconstruct data via pattern-matching
volume :: Cuboid -> Double
volume c = case c of
MkCuboid l d h -> l * d * h
case e of Ctor x y z -> e1 is read as as
IF - e evaluates to a value that matches the pattern Ctor vx vy vz
THEN - evaluate e1 after naming x := vx, y := vy, z := vz
Pattern matching on Function Inputs
Very common to do matching on function inputs
volume :: Cuboid -> Double
volume c = case c of
MkCuboid l d h -> l * d * h
area :: Circle -> Double
area a = case a of
MkCircle x y r -> pi * r * r
So Haskell allows a nicer syntax: patterns in the arguments
volume :: Cuboid -> Double
volume (MkCuboid l d h) = l * d * h
area :: Circle -> Double
area (MkCircle x y r) = pi * r * r
Nice syntax plus the compiler saves us from mixing up values!
But … what if we need to mix up values?
Suppose I need to represent a list of shapes
- Some
Circles - Some
Cuboids
What is the problem with shapes as defined below?
Where we have defined
circ1 :: CircleT
circ1 = MkCircle 0 0 100 -- ^ circle at "origin" with radius 100
cub1 :: Cuboid
cub1 = MkCuboid 10 20 30 -- ^ cuboid with length=10, depth=20, height=30
Problem: All list elements must have the same type
Solution???
QUIZ: Variant (aka Union) Types
Lets create a single type that can represent both kinds of shapes!
data Shape
= MkCircle Double Double Double -- ^ Circle at x, y with radius r
| MkCuboid Double Double Double -- ^ Cuboid with length, depth, height
What is the type of MkCircle 0 0 100 ?
A. Shape
B. Circle
C. (Double, Double, Double)
Each Data Constructor of Shape has a different type
When we define a data type like the below
data Shape
= MkCircle Double Double Double -- ^ Circle at x, y with radius r
| MkCuboid Double Double Double -- ^ Cuboid with length, depth, height
We get multiple constructors for Shape
MkCircle :: Double -> Double -> Double -> Shape
MkCuboid :: Double -> Double -> Double -> Shape
Now we can create collections of Shape
Now we can define
circ2 :: Shape
circ2 = MkCircle 0 0 100 -- ^ circle at "origin" with radius 100
cub2 :: Shape
cub2 = MkCuboid 10 20 30 -- ^ cuboid with length=10, depth=20, height=30
and then define collections of Shapes
shapes :: [Shape]
shapes = [circ1, cub1]
EXERCISE
Lets define a type for 2D shapes
data Shape2D
= MkRect Double Double -- ^ 'MkRect w h' is a rectangle with width 'w', height 'h'
| MkCirc Double -- ^ 'MkCirc r' is a circle with radius 'r'
| MkPoly [Vertex] -- ^ 'MkPoly [v1,...,vn]' is a polygon with vertices at 'v1...vn'
type Vertex = (Double, Double)
Write a function to compute the area of a Shape2D
area2D :: Shape2D -> Double
area2D s = ???
HINT
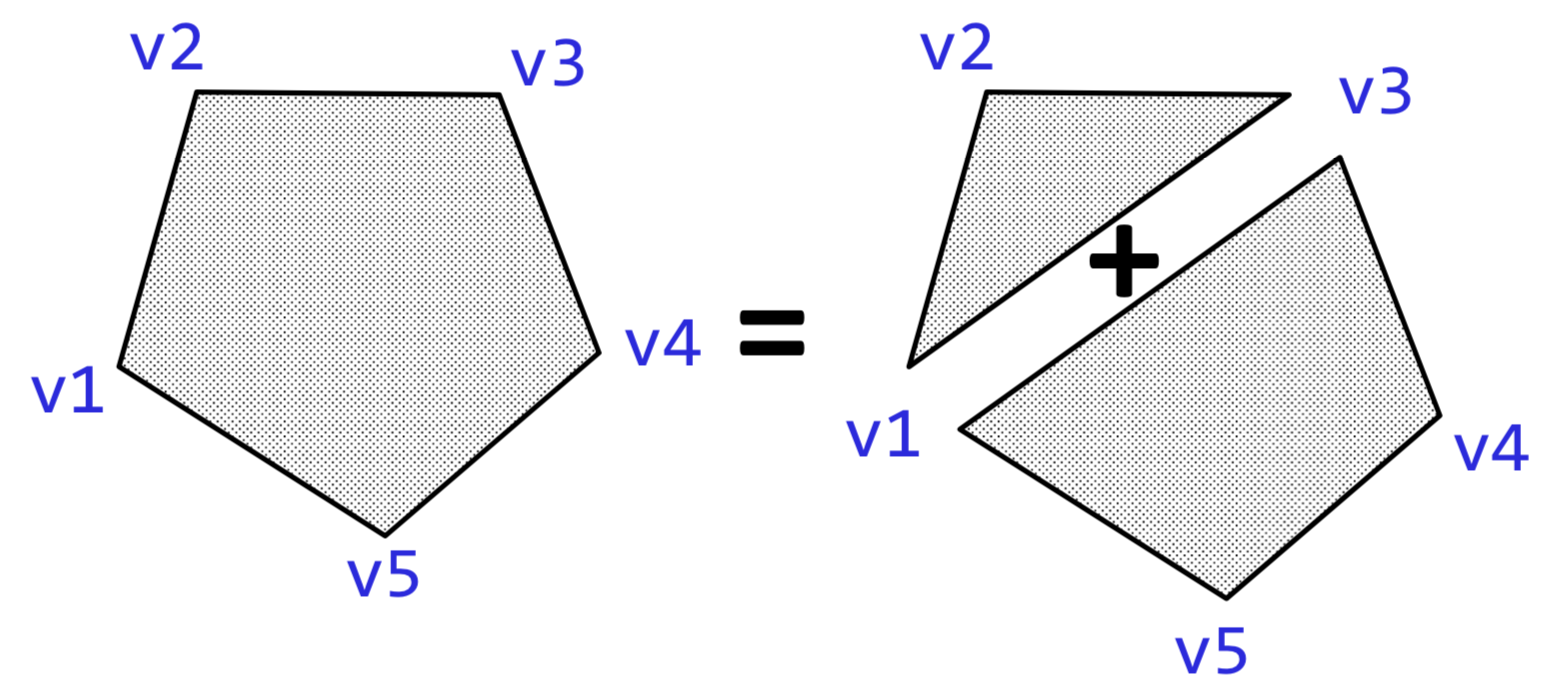
Area of a polygon
You may want to use this helper that computes the area of a triangle at v1, v2, v3
areaTriangle :: Vertex -> Vertex -> Vertex -> Double
areaTriangle v1 v2 v3 = sqrt (s * (s - s1) * (s - s2) * (s - s3))
where
s = (s1 + s2 + s3) / 2
s1 = distance v1 v2
s2 = distance v2 v3
s3 = distance v3 v1
distance :: Vertex -> Vertex -> Double
distance (x1, y1) (x2, y2) = sqrt ((x2 - x1) ** 2 + (y2 - y1) ** 2)
Polymorphic Data Structures
Next, lets see polymorphic data types
which contain many kinds of values.
Recap: Data Types
Recall that Haskell allows you to create brand new data types
data Shape
= MkRect Double Double
| MkPoly [(Double, Double)]
QUIZ
What is the type of MkRect ?
data Shape
= MkRect Double Double
| MkPoly [(Double, Double)]
a. Shape
b. Double
c. Double -> Double -> Shape
d. (Double, Double) -> Shape
e. [(Double, Double)] -> Shape
Tagged Boxes
Values of this type are either two doubles tagged with Rectangle
>>> :type (Rectangle 4.5 1.2)
(Rectangle 4.5 1.2) :: Shape
or a list of pairs of Double values tagged with Polygon
ghci> :type (Polygon [(1, 1), (2, 2), (3, 3)])
(Polygon [(1, 1), (2, 2), (3, 3)]) :: Shape
Data values inside special Tagged Boxes

Datatypes are Boxed-and-Tagged Values
Recursive Data Types
We can define datatypes recursively too
data IntList
= INil -- ^ empty list
| ICons Int IntList -- ^ list with "hd" Int and "tl" IntList
deriving (Show)
(Ignore the bit about deriving for now.)
QUIZ
data IntList
= INil -- ^ empty list
| ICons Int IntList -- ^ list with "hd" Int and "tl" IntList
deriving (Show)
What is the type of ICons ?
A. Int -> IntList -> List
B. IntList
C. Int -> IntList -> IntList
D. Int -> List -> IntList
E. IntList -> IntList
Constructing IntList
Can only build IntList via constructors.
>>> :type INil
INil:: IntList
>>> :type ICons
ICons :: Int -> IntList -> IntList
EXERCISE
Write down a representation of type IntList of the list of three numbers 1, 2 and 3.
list_1_2_3 :: IntList
list_1_2_3 = ???
Hint Recursion means boxes within boxes
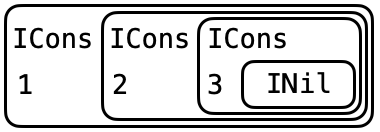
Recursively Nested Boxes
Trees: Multiple Recursive Occurrences
We can represent Int trees like
data IntTree
= ILeaf Int -- ^ single "leaf" w/ an Int
| INode IntTree IntTree -- ^ internal "node" w/ 2 sub-trees
deriving (Show)
A leaf is a box containing an Int tagged ILeaf e.g.
>>> it1 = ILeaf 1
>>> it2 = ILeaf 2
A node is a box containing two sub-trees tagged INode e.g.
>>> itt = INode (ILeaf 1) (ILeaf 2)
>>> itt' = INode itt itt
>>> INode itt' itt'
INode (INode (ILeaf 1) (ILeaf 2)) (INode (ILeaf 1) (ILeaf 2))
Multiple Branching Factors
e.g. 2-3 trees
data Int23T
= ILeaf0
| INode2 Int Int23T Int23T
| INode3 Int Int23T Int23T Int23T
deriving (Show)
An example value of type Int23T would be
i23t :: Int23T
i23t = INode3 0 t t t
where t = INode2 1 ILeaf0 ILeaf0
which looks like
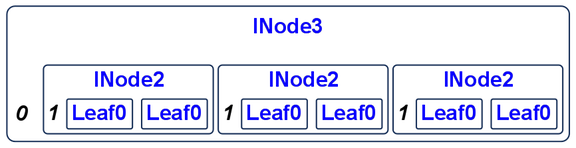
Integer 2-3 Tree
Parameterized Types
We can define CharList or DoubleList - versions of IntList for Char and Double as
data CharList
= CNil
| CCons Char CharList
deriving (Show)
data DoubleList
= DNil
| DCons Char DoubleList
deriving (Show)
Don’t Repeat Yourself!
Don’t repeat definitions - Instead reuse the list structure across all types!
Find abstract data patterns by
- identifying the different parts and
- refactor those into parameters
A Refactored List
Here are the three types: What is common? What is different?
data IList = INil | ICons Int IList
data CList = CNil | CCons Char CList
data DList = DNil | DCons Double DList
Common: Nil/Cons structure
Different: type of each “head” element
Refactored using Type Parameter
data List a = Nil | Cons a (List a)
Recover original types as instances of List
type IntList = List Int
type CharList = List Char
type DoubleList = List Double
Polymorphic Data has Polymorphic Constructors
Look at the types of the constructors
>>> :type Nil
Nil :: List a
That is, the Empty tag is a value of any kind of list, and
>>> :type Cons
Cons :: a -> List a -> List a
Cons takes an a and a List a and returns a List a.
cList :: List Char -- list where 'a' = 'Char'
cList = Cons 'a' (Cons 'b' (Cons 'c' Nil))
iList :: List Int -- list where 'a' = 'Int'
iList = Cons 1 (Cons 2 (Cons 3 Nil))
dList :: List Double -- list where 'a' = 'Double'
dList = Cons 1.1 (Cons 2.2 (Cons 3.3 Nil))
Polymorphic Function over Polymorphic Data
Lets write the list length function
len :: List a -> Int
len Nil = 0
len (Cons x xs) = 1 + len xs
len doesn’t care about the actual values in the list - only “counts” the number of Cons constructors
Hence len :: List a -> Int
- we can call
lenon any kind of list.
>>> len [1.1, 2.2, 3.3, 4.4] -- a := Double
4
>>> len "mmm donuts!" -- a := Char
11
>>> len [[1], [1,2], [1,2,3]] -- a := ???
3
Built-in Lists?
This is exactly how Haskell’s “built-in” lists are defined:
data [a] = [] | (:) a [a]
data List a = Nil | Cons a (List a)
Nilis called[]Consis called:
Many list manipulating functions e.g. in [Data.List][1] are polymorphic - Can be reused across all kinds of lists.
(++) :: [a] -> [a] -> [a]
head :: [a] -> a
tail :: [a] -> [a]
Generalizing Other Data Types
Polymorphic trees
data Tree a
= Leaf a
| Node (Tree a) (Tree a)
deriving (Show)
Polymorphic 2-3 trees
data Tree23 a
= Leaf0
| Node2 (Tree23 a) (Tree23 a)
| Node3 (Tree23 a) (Tree23 a) (Tree23 a)
deriving (Show)
Kinds
List a corresponds to lists of values of type a.
If a is the type parameter, then what is List?
A type-constructor that - takes as input a type a - returns as output the type List a
But wait, if List is a type-constructor then what is its “type”?
- A kind is the “type” of a type.
>>> :kind Int
Int :: *
>>> :kind Char
Char :: *
>>> :kind Bool
Bool :: *
Thus, List is a function from any “type” to any other “type”, and so
>>> :kind List
List :: * -> *
QUIZ
What is the kind of ->? That, is what does GHCi say if we type
A. *
B. * -> *
C. * -> * -> *
We will not dwell too much on this now.
As you might imagine, they allow for all sorts of abstractions over data.
If interested, see this for more information about kinds.